An addendum to squares - rectangles!

This post is going to be rather random, but I made this discovery the other night, and so I wanted to write it out.

Quite a while ago now, when I was back in high school, I was fascinated with those grid squares that ask you to say how many squares of any size are within that grid.
I managed to figure out that if you have a grid of size x, where x is the number of squares along the side of the square, then the number of squares of any size you can find in the grid is equal to:
x^2 + (x-1)^2 + (x-2)^2 + ....... + 1. It's a sum of diminishing square numbers.



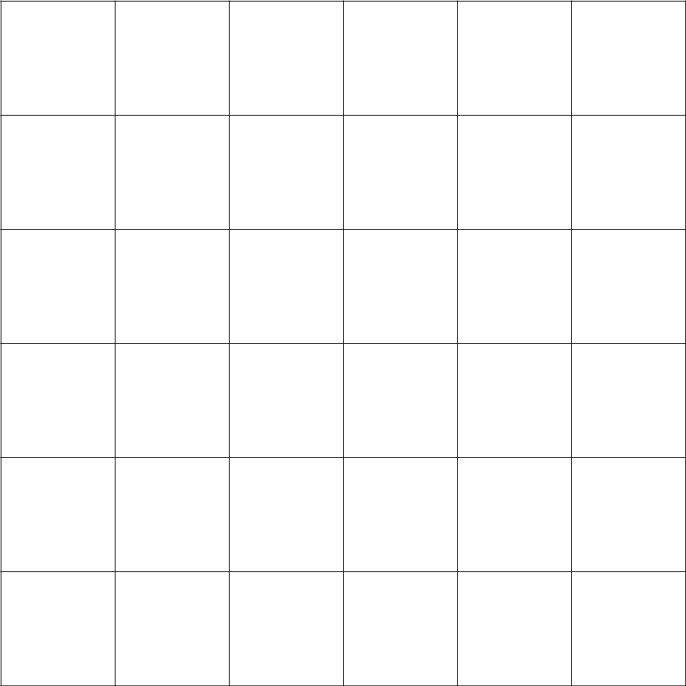
So, in the above grid, with size 6, that's 6^2 + 5^2 + 4^2 + 3^2 + 2^2 + 1^2, or 36 + 25 + 16 + 9 + 4 + 1, which is 91. (The contracted formula is (x(x+1)(2x+1))/6, but that's trickier to remember.)
I then tried to do it with a triangle grid....but that problem turned out to be rather more difficult and complicated.

But, what I did figure out randomly the other night in my sleep was......rectangles! And they're actually surprisingly simple.

Say you have a rectangle grid, with sides of length a and b. The number of unit squares in the grid is pretty obvious - it's ab. So then, I wondered if I could almost substitute a and b into the original equation I had - and, it turns out, I can! So, we end up with this:

ab + (a-1)(b-1) + (a-2)(b-2) + .....

The only difference for this formula is that it doesn't have 1 as the last number. In the last bracket, either a or b will equal 1, but not both, otherwise it would be a square! And if you take away 1 again, obviously you get zero, which multiplies to give itself again, so you're no longer adding any more.

But I'm quite happy with this result! I've already tried it out with a few rectangle grids, and it seems to be working really well so far. I'm pretty sure that it will always work, but let me know if you find a corner case!
What I'm not sure of is how this could potentially be factored down. I can't really create a series to search for, because rectangles can have all sorts of ratios. So this might be as far as I can get with it for now, but I'm okay with that.